03-3 특성 공학과 규제

6 분 소요

03-3 특성 공학과 규제

여러 특성을 사용한 다중 회귀에 대해 배우고, 복잡한 모델의 과대적합을 막기 위한 릿지와 라쏘 회귀를 배움

💡용어 정리💡

❓ 다중 회귀 ➡️ 여러 개의 특성을 사용한 선형 회귀

❓ 특성 공학 ➡️ 기존의 특성을 사용해 새로운 특성을 뽑아내는 작업

❓ 규제 ➡️ 머신러닝 모델이 훈련 세트를 너무 과도하게 학습하지 못하도록 훼방하는 것

–> 즉, 모델이 훈련 세트에 과대적합되지 않도록 하는 것!

( 선형 회귀 모델에서는 특성에 곱해지는 계수(기울기)를 작게 만듦 )

❓ 하이퍼파라미터 ➡️ 릿지 라쏘의 alpha값! 모델이 학습할 수 없고, 사람이 알려줘야 하는 파라미터

1) 판다스 이용하여 농어 데이터 불러오기 –> 특성 데이터셋 생성

pandas –> 데이터 분석 라이브러리
데이터프레임 –> pandas의 핵심 데이터구조

# 농어 데이터를 읽기 위한 판다스 임포트
import pandas as pd

# pd.read_scv()에 데이터의 주소를 넣으면 데이터프레임 생성
df = pd.read_csv('https://bit.ly/perch_csv_data')

# to_numpy()로 넘파이 배열로 변환
perch_full = df.to_numpy()
print(perch_full)

실행결과)

[[ 8.4   2.11  1.41]
 [13.7   3.53  2.  ]
 [15.    3.82  2.43]
 [16.2   4.59  2.63]
 [17.4   4.59  2.94]
 [18.    5.22  3.32]
 [18.7   5.2   3.12]
 [19.    5.64  3.05]
 [19.6   5.14  3.04]
 [20.    5.08  2.77]
 [21.    5.69  3.56]
 [21.    5.92  3.31]
 [21.    5.69  3.67]
 [21.3   6.38  3.53]
 [22.    6.11  3.41]
 [22.    5.64  3.52]
 [22.    6.11  3.52]
 [22.    5.88  3.52]
 [22.    5.52  4.  ]
 [22.5   5.86  3.62]
 [22.5   6.79  3.62]
 [22.7   5.95  3.63]
 [23.    5.22  3.63]
 [23.5   6.28  3.72]
 [24.    7.29  3.72]
 [24.    6.38  3.82]
 [24.6   6.73  4.17]
 [25.    6.44  3.68]
 [25.6   6.56  4.24]
 [26.5   7.17  4.14]
 [27.3   8.32  5.14]
 [27.5   7.17  4.34]
 [27.5   7.05  4.34]
 [27.5   7.28  4.57]
 [28.    7.82  4.2 ]
 [28.7   7.59  4.64]
 [30.    7.62  4.77]
 [32.8  10.03  6.02]
 [34.5  10.26  6.39]
 [35.   11.49  7.8 ]
 [36.5  10.88  6.86]
 [36.   10.61  6.74]
 [37.   10.84  6.26]
 [37.   10.57  6.37]
 [39.   11.14  7.49]
 [39.   11.14  6.  ]
 [39.   12.43  7.35]
 [40.   11.93  7.11]
 [40.   11.73  7.22]
 [40.   12.38  7.46]
 [40.   11.14  6.63]
 [42.   12.8   6.87]
 [43.   11.93  7.28]
 [43.   12.51  7.42]
 [43.5  12.6   8.14]
 [44.   12.49  7.6 ]]

2) 농어 무게 데이터 입력 –> 타깃 테이터셋 생성

import numpy as np
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
       115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
       150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
       218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
       556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
       850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
       1000.0])

3) perch_full과 perch_weight를 훈련 세트와 테스트 세트로 분할

from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(perch_full, perch_weight, random_state=42)

변환기 PolynomialFeatures 클래스를 이용한 데이터 변환 테스트

사이킷런의 모델 클레스 메서드 vs 사이킷런의 변환기 클래스 메서드

fit(), score(), predict() vs fit(), transform()

fit() –> 새롭게 만들 특성 조합을 찾음
transform() –> 실제로 fit()을 바탕으로 데이터 변환
결과는 각 특성을 제곱한 항과 특성끼리 서로 곱한 항을 추가함

(2, 3이 특성 –> 2 * 3 = 6, 2^2 = 4, 3^2 = 9 추가)

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(include_bias=False) # 절편을 위한 항 제거

# 입력 데이터(특성)만 존재하며 타깃 데이터는 존재하지xx
poly.fit([[2, 3]])
# 훈련을 해야 변환이 가능함! 꼭 fit() -> transform()
print(poly.transform([[2, 3]]))

실행결과)

[[2. 3. 4. 6. 9.]]

4) 변환기를 이용해 데이터 변환

poly = PolynomialFeatures(include_bias=False)

poly.fit(train_input)

train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)

# 변환한 데이터 train_poly의 크기 확인
print(train_poly.shape)

실행결과)

(42, 9)

5) 다중 회귀 모델 훈련

특성이 늘어날수록 선형 회귀의 능력은 강해짐!

from sklearn.linear_model import LinearRegression
lr = LinearRegression()

# 변환기와 다르게 훈련하기 위한 fit() 실행
lr.fit(train_poly, train_target)

# train R^2 > test R^2 --> 과소적합 해결!
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))

실행결과)

0.9903183436982124
0.9714559911594134

변환기 클래스를 이용하여 더 많은 특성 추가

# 5제곱 까지의 특성 추가
poly = PolynomialFeatures(degree=5, include_bias=False) # degree 매개변수를 이용해 필요한 고차항의 최대 차수 지정 가능!

poly.fit(train_input)

# 데이터 변환
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)

# train_poly 배열의 열의 개수 = 특성의 개수(55개), 샘플 개수(42) 따라서, 샘플 개수 < 특성의 개수
print(train_poly.shape)

실행결과)

(42, 55)

5제곱 변환된 데이터를 이용하여 모델 훈련

# 변환된 데이터를 이용하여(5제곱 특성) 모델 훈련
lr.fit(train_poly, train_target)

# train R^2 >>>>>> test R^2 --> 과대적합
# 너무 많아진 특성 때문! 따라서, 특성 개수 조절 필요!
# p.159 그림 참조
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))

실행결과)

0.9999999999991097
-144.40579242684848

5제곱 변환된 데이터의 정규화를 위한 객체 훈련과 변환

평균과 표준편차 생성을 위해 변환기 클래스 사용 –> StandardScaler()

# 정규화(특성을 표준점수로 바꾼 일)를 하기위한 변환기 클래스 사용
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()

# 훈련 세트로 객체 훈련
# 훈련 세트에서 학습한 평균과 표준편차는 ss의 mean_과 scale_ 속성에 저장됨(특성마다 계산하므로 55개의 평균과 표준편차가 존재!)
ss.fit(train_poly)

# 훈련된 객체를 변환기로 변환 --> 꼭꼭!! 훈련 세트로 학습한 변환기를 사용하여 테스트 세트까지 변환!
train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)

선형 회귀 모델에 규제 추가 –> 릿지 & 라쏘

릿지 –> 계수를 제곱한 값을 기준으로 규제 적용
라쏘 –> 계수의 절댓값을 기준으로 규제 적용(아예 0으로 만들 수 있음)
릿지와 라쏘 모델 둘 다 규제의 양을 임의로 조절 가능

–> 모델 객체를 만들 때 alpha 매개변수로 규제의 강도 조절!

( alpha 값이 크면 규제 강도가 세짐 -> 계수 값을 더 줄여서 과소적합 유도! )

( 반대로, alpha 값이 작으면 선형 회귀 모델과 유사해짐 -> 과대적합 가능성 up )

(1)-1 릿지 알고리즘 생성 및 훈련

# 규제를 가하기 위한 릿지 알고리즘
from sklearn.linear_model import Ridge
ridge = Ridge()

# 모델 훈련
ridge.fit(train_scaled, train_target)

# 규제하기 전 R^2 점수보다 조금 낮음!
print(ridge.score(train_scaled, train_target))
print(ridge.score(test_scaled, test_target)) # 테스트 점수 정상으로 돌아옴!

실행결과)

0.9896101671037343
0.9790693977615397	

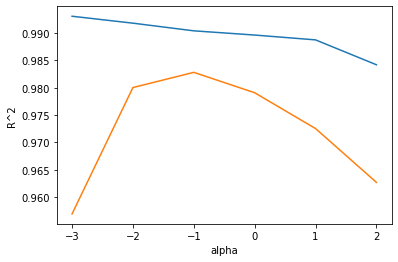
(1)-2 릿지 모델의 alpha 값에 대한 R^2 값의 그래프 생성

왜 그래프를 그리나? 적절한 alpha 값을 찾기 위해!
훈련 세트와 테스트 세트의 점수가 가장 가까운 지점이 최적의 alpha 값!

import matplotlib.pyplot as plt

# alpha 값을 바꿀 때마다 score()의 결과를 저장 할 리스트 생성!
train_score = []
test_score = []

# alpha 값을 0.001에서 10배씩 늘려가며 릿지 회귀 모델 훈련!
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:

  # 릿지 모델 만듦
  ridge = Ridge(alpha=alpha)

  # 릿지 모델 훈련
  ridge.fit(train_scaled, train_target)

  # 훈련 점수와 테스트 점수 저장
  train_score.append(ridge.score(train_scaled, train_target))
  test_score.append(ridge.score(test_scaled, test_target))

# alpha_list에 있는 6개의 값을 동일한 간격으로 나타내기 위해 지수 표현!
plt.plot(np.log10(alpha_list), train_score) # 파랑 라인
plt.plot(np.log10(alpha_list), test_score) # 주황 라인

plt.xlabel('alpha')
plt.ylabel('R^2')

# 왼쪽은 훈련 세트와 테스트 세트의 점수 차이가 매우 큼! --> 과대적합
# 오른쪽은 두 세트의 점수가 모두 낮아짐 --> 과소적합
# 적절한 alpha? 두 그래프가 가장 가깝고, 테스트 점수가 가장 높은 --> -1 (10^-1=0.1)
plt.show()

실행결과)

(1)-3 릿지 최종 모델 훈련 –> alpha의 적절한 값 찾음

# alpha=0.1로 최종 모델 훈련
ridge = Ridge(alpha=0.1) # 그래프로 적절한 alpha 값 찾음!

ridge.fit(train_scaled, train_target)

print(ridge.score(train_scaled, train_target))
print(ridge.score(test_scaled, test_target))

(2)-1 라쏘 알고리즘 생성 및 훈련

from sklearn.linear_model import Lasso
lasso = Lasso()

lasso.fit(train_scaled, train_target)

print(lasso.score(train_scaled, train_target))
print(lasso.score(test_scaled, test_target))

실행결과)

0.989789897208096

(2)-2 라쏘 모델의 alpha 값에 대한 R^2 값의 그래프 생성

train_score = []
test_score = []
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
  
  # 라쏘 모델 생성
  lasso = Lasso(alpha=alpha, max_iter=10000)

  # 라쏘 모델 훈련
  lasso.fit(train_scaled, train_target)

  # 훈련 점수와 테스트 점수 저장
  train_score.append(lasso.score(train_scaled, train_target))
  test_score.append(lasso.score(test_scaled, test_target))

실행결과)

/usr/local/lib/python3.7/dist-packages/sklearn/linear_model/_coordinate_descent.py:648: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations, check the scale of the features or consider increasing regularisation. Duality gap: 1.878e+04, tolerance: 5.183e+02
  coef_, l1_reg, l2_reg, X, y, max_iter, tol, rng, random, positive
/usr/local/lib/python3.7/dist-packages/sklearn/linear_model/_coordinate_descent.py:648: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations, check the scale of the features or consider increasing regularisation. Duality gap: 1.297e+04, tolerance: 5.183e+02
  coef_, l1_reg, l2_reg, X, y, max_iter, tol, rng, random, positive

# x축을 로그 스케일로 변경
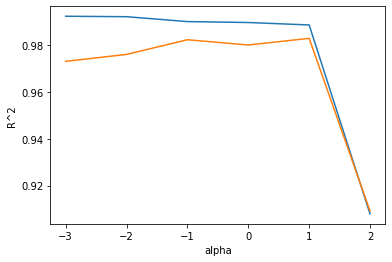
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)

plt.xlabel('alpha')
plt.ylabel('R^2')

# 왼쪽 --> 과대적합
# 오른쪽 --> 훈련 세트와 테스트 세트의 점수가 아주 크게 떨어짐, 과소적합!
# 적절한 alpha=1, 10^1=10
plt.show()

실행결과)

(2)-3 라쏘 최종 모델 훈련 –> alpha의 적절한 값 찾음

# 라쏘 최종 모델 훈련
lasso = Lasso(alpha=10)

lasso.fit(train_scaled, train_target)

print(lasso.score(train_scaled, train_target))
print(lasso.score(test_scaled, test_target))

실행결과)

0.9888067471131867
0.9824470598706695

라쏘 모델의 계수 중 0인 것 찾기

넘파이 배열에 비교 연산자 사용 –> true 또는 false로 표시
np.sum() –> true->1, false->0 으로 계산!

print(np.sum(lasso.coef_ == 0)) # np.sum()는 배열을 모두 더한 값 반환
# 특성은 55개 주입했지만, 사용한 특성은 15개 --> 유용한 특성을 골라내는 용도로 사용 가능!

실행결과)

Twitter Facebook LinkedIn

Chae Yeon Jang

03-3 특성 공학과 규제

03-3 특성 공학과 규제

여러 특성을 사용한 다중 회귀에 대해 배우고, 복잡한 모델의 과대적합을 막기 위한 릿지와 라쏘 회귀를 배움

공유하기

댓글남기기

참고

< NFT 기반 디지털 자산 거래를 위한 블록체인 합의 연구 > 논문 분석

GitBlog) Utterance 댓글 설정

GitBlog) Favicon(파비콘) 설정

05-1 결정 트리